Aryabhatta (or Aryabhata)(476 – 550 CE) was an Indian mathematician and astronomer who is regarded as a towering figure in both these fields. Some of his works have been lost through the ages but his influence may be seen in the works of succeeding Indian mathematicians who frequently refer to his works. Among other things, Aryabhata calculated the closest approximate value of pi till that time; was the first known person to solve Diophantine equations; was first to explain that moon and planets shine due to reflected sunlight; and made major contributions to the fields of Trigonometry and Algebra. Aryabhatta was one of the greatest mathematicians in history and a pioneer in the classical age of Indian mathematics and astronomy. Know more about his contributions through his 10 major achievements.
#1 HE WROTE THE HUGELY INFLUENTIAL ARYABHATIYA
Although Aryabhatta wrote several treatises, Aryabhatiya is his only known surviving work and it is widely regarded as his magnum opus. It is primarily an astronomical treatise written in 121 verses. Its mathematical section contains 33 verses giving 66 mathematical rules. Aryabhatiya is divided into four chapters: Gitikapada (13 verses), Ganitapada (33 verses), Kalakriyapada (25 verses) and Golapada (50 verses). Among other things, Aryabhatiya contains a systematic treatment of the position of the planets in space; the nature of the Solar System; and the causes of eclipses of the Sun and the Moon. The mathematical part of the Aryabhatiya covers arithmetic, algebra, plane trigonometry and spherical trigonometry. It also contains continued fractions, quadratic equations, sums of power series and a table of sines. Aryabhatiya was a hugely influential text and it presents many ideas that are foundational to modern astronomy and mathematics.

#2 HE IS THE FIRST KNOWN PERSON TO SOLVE DIOPHANTINE EQUATIONS
A Diophantine equation is an equation that has more than one unknown integer. A simple Diophantine equation would be ax + by = c. In this equation a, b and c are given integers; and x and y unknown integers. Aryabhatiya is the earliest known work which examines integer solutions to Diophantine equations of the form by = ax + c and by = ax – c. For this purpose, Aryabhata promptly introduced a new and popular method, known as the Kuttaka method. The word kuttaka means “to pulverise” and Aryabhata’s method was based around a recursive algorithm which involved writing the original factors in smaller numbers. Diophantine equations were considered very difficult to solve at the time and the Kuttaka method quickly became very popular. It is still the standard method of solving such equations.
#3 HE MADE MAJOR CONTRIBUTIONS TO TRIGONOMETRY AND ALGEBRA
Aryabhatiya provides simple solutions to complex mathematical problems of the time like summing the first n integers, the squares of these integers and also their cubes. Furthermore, Aryabhatta correctly calculated the areas of a triangle and of a circle. For example in Ganitapadam his writings can be translated as “for a triangle, the result of a perpendicular with the half-side is the area.” In trigonometry, Aryabhatta gave a table of sines calculating the approximate values at intervals of 90°/24 = 3° 45′. In order to do this he used a formula for sin(n + 1)x – sin nx in terms of sin nx and sin (n – 1)x. He was also the one to introduce the versine (versin = 1 – cosine) into trigonometry.
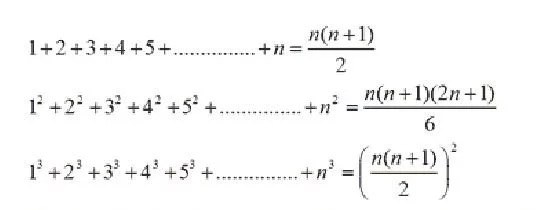
#4 HE PROBABLY UNDERSTOOD THE CONCEPT OF ZERO
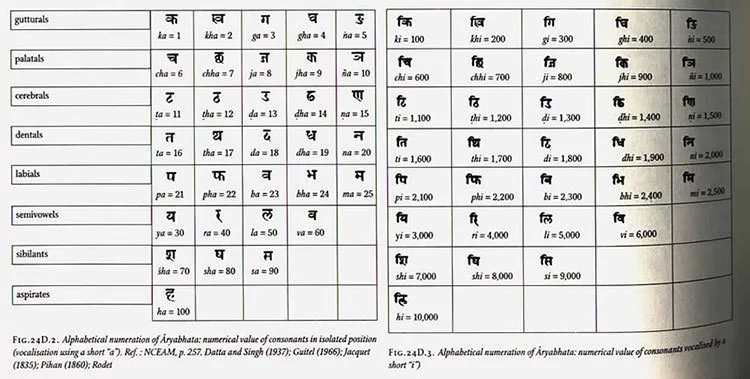
In Aryabhatiya, Aryabhatta introduced a system of numerals in which he used letters of the Indian alphabet to denote numbers. His numeral system allowed numbers up to 1018 to be represented with an alphabetical notation. It is considered that Aryabhatta was familiar with the concept of zero and the place value system. Although nowhere in his works did he use the symbol of zero, French mathematician Georges Ifrah argues that the existence and knowledge of zero were implicit in Aryabhata’s place-value system as a place holder for the powers of 10 with null coefficients. Ifrah based his supposition on the following two facts: “first, the invention of his alphabetical counting system would have been impossible without zero or the place-value system; secondly, he carries out calculations on square and cubic roots which are impossible if the numbers in question are not written according to the place-value system and zero.” This is an incredible achievement for the time and one of the earliest proper understanding of the concept of zero, which is fundamental to mathematics.
#5 HE CALCULATED THE CLOSEST APPROXIMATE VALUE OF PI TILL THAT TIME
One of the most important achievements of Aryabhatta is giving an approximate value of Pi (π). An account of this is found in the second part of Aryabhatiyam where he explains “Add four to 100, multiply by eight, and then add 62,000. By this rule, the circumference of a circle with a diameter of 20,000 can be approached.” This calculation gives the vale of pi to be 62832/20000 = 3.1416, reflecting an accuracy of 5 significant digits. In fact π = 3.14159265 correct to 8 places. Aryabhatta’s value of π is a very close approximation to the modern value and the most accurate among those of the ancients. Furthermore, it is also considered that Aryabhata knew that the value of Pi was irrational. This was an amazing discovery since the value of Pi was proved to be irrational only in the year 1761 by Swiss mathematician Johann Heinrich Lambert.

#6 HE MADE INCREDIBLY ACCURATE CALCULATIONS OF THE LENGTH OF THE DAY AND THE YEAR
Aryabhata calculated the circumference of the Earth as 39,968 kilometers while the actual circumference is 40,075 kilometers. Thus Aryabhatta’s value of the size of the earth is only 0.2% smaller than the actual size. Aryabhata also put forth impressive calculations regarding the sidereal rotation (rotation calculated by referencing the position of the fixed stars) of the Earth. He calculated it as 23 hours, 56 minutes and 4.1 seconds; this is unbelievably close to the modern-day calculated value of 23 hours, 56 minutes and 4.091 seconds, representing an error of merely 0.09 seconds! Similarly, Aryabhata calculated the value of the sidereal year to be 365.25858 days, an error of just 3 minutes and 20 seconds as compared to the actual length of a year calculated today, which comes out to be 365.25636 days. These calculations by Aryabhatta were one of the most accurate calculations in the world till that time.
#7 HE WAS FIRST TO EXPLAIN THAT MOON AND PLANETS SHINE DUE TO REFLECTED SUNLIGHT
Even with the lack of any accurate astronomical instruments at the time, Aryabhata was able to successfully deduce that the Earth is round and revolves around its axis. Furthermore, he connected this with the existence of the day and night. Aryabhata used a geocentric model for the solar system, in which the Sun and Moon are each carried by epicycles which in turn revolve around the Earth. However, despite using a geocentric model, Aryabhata correctly explained how the moons and planets have no light of their own but shine due to the reflection of sunlight. Furthermore he corrected the flawed belief that eclipses are caused because of the shadows cast by the Earth and Moon and instead explained the correct causes of eclipses. The computational model of Aryabhata was so accurate that in the 18th Century, scientist Guillaume Le Gentil found his calculations regarding the duration of the lunar eclipse of 30th August 1765 to be short by only 41 seconds!

#8 HE EXPLAINED HOW MOVEMENT OF CELESTIAL BODIES WAS DUE TO ROTATION OF THE EARTH
Aryabhata explained how the Earth moves around its axis and he also explained how the apparent movements of stars in the night sky is, in fact, a relative motion that is caused by the rotation of the Earth. This bashed the popularly accepted view of the time that this was caused by the rotation of the sky. All this and more is mentioned in the very first chapter of Aryabhatiya where Aryabhata calculates the number of rotations of the Earth in a Yuga (one of the four eras defined in Hinduism). He writes “In the same way that someone in a boat going forward sees an unmoving [object] going backwards, so [someone] on the equator sees the unmoving stars going uniformly westward. The cause of rising and setting [is that] the sphere of the stars together with the planets [apparently?] turns due west at the equator, constantly pushed by the cosmic wind.”

#9 HE AUTHORED AN INFLUENTIAL TEXT TITLED ARYA-SIDDHANTA
Aryabhata also penned another major work on astronomical computations, known as the Arya-Siddhanta. However this has been lost through the ages. The Arya-Siddhanta came into light primarily through the works of astronomer Viharamitra, who was Aryabhata’s contemporary. Later, it was also picked up by famous mathematicians such as Brahmagupta and Bhaskara I. Arya-Siddhanta makes use of the midnight-day reckoning and is based on the older Surya-Siddhanta. The work covers some of the major astronomical instruments of the time including the shadow instrument; angle measuring devices; semicircular and circular devices; umbrella-shaped device; a cylindrical stick Yasti-yantra; and water clocks that include bow-shaped and cylindrical designs. Additionally, Aryabhata has also been credited with setting up an observatory at the Sun Temple in Taregana.

#10 HE IS A TOWERING FIGURE IN MATHEMATICS AND ASTRONOMY
Aryabhatta was the first of the great astronomers of the classical age of India. He had a huge influence on Indian mathematics and astronomy with his works providing the basis for the achievements of future figures in these fields. Furthermore, Aryabhata’s work was well known throughout the Islamic world and played a part in the Islamic Golden Age. Particularly his astronomical calculation methods, along with the trigonometric tables, were widely used in the Islamic world and used to compute many Arabic astronomical tables (zijes). The work of Aryabhatta was not known to the west for centuries after his death. However, when his work was translated to Latin in the 1200s, it became very influential and many of his ideas were utilized by European mathematicians and astronomers.


How did Aryabhata calculate the circumference of the Earth as 39,968 kilometers? Is it somewhat similar to the method of Greek astronomer Eratosthenes?