Leonardo Pisano (Leonardo of Pisa), better known as Fibonacci, was an Italian mathematician who is most famous for his Fibonacci sequence and for popularizing the Hindu-Arabic numeral system in Europe. Here are 10 interesting facts about his life and accomplishments; and also on the Fibonacci sequence, its relation to golden ratio and its prevalence in nature.
#1 HE LEARNED THE HINDU-ARABIC NUMERAL SYSTEM IN BUGIA
Leonardo Fibonacci was born around 1170 in Pisa, Italy. His father Guglielmo Bonacci was a wealthy Italian merchant, who represented merchants of the Republic of Pisa who were trading in Bugia (now Béjaïa) in Algeria, North Africa. It was in Bugia that Leonardo first learned the Hindu–Arabic numeral system. He traveled extensively around the Mediterranean till around 1200 after which he returned to Pisa. During his travels he met numerous merchants and studied different numerical systems and methods of calculation.

#2 FIBONACCI POPULARIZED THE HINDU-ARABIC NUMERAL SYSTEM IN EUROPE
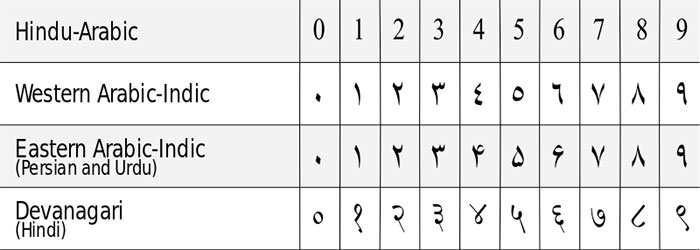
Fibonacci realized the numerous advantages of the Hindu-Arabic numeral system. Although today the system is the most common representation of numbers, at the time it was known only to a few scholars in Europe. In 1202, Fibonacci completed Liber Abaci (Book of Calculation), a book on the Hindu-Arabic numerals and their use in arithmetical operations and practical problems. Liber Abaci was widely copied and imitated; and was instrumental in popularizing the Hindu–Arabic numeral system in Europe.
#3 BOOK OF SQUARES IS CONSIDERED HIS MASTERPIECE
In 1225, Fibonacci completed Liber Quadratorum (Book of Square Numbers) which is considered his masterpiece. The book is a collection of theorems and examines several topics in number theory. Among other things, it contains the solution to the congruum problem, methods to find Pythogorean triples, Fibonacci’s identity and the fact that the sum of all odd integers is n^2. However, Fibonacci’s contributions to number theory went largely unnoticed.

#4 HE MADE AN IMPORTANT CONTRIBUTION IN SPREADING DECIMAL NUMERALS
The year of Fibonacci’s death is not known but it is estimated to be somewhere between 1240 and 1250. He was well known during his time, became a guest of Emperor Frederick II and was honored by the Republic of Pisa. Before Fibonacci, Europe used Roman Numerals which make modern mathematics almost impossible. He advocated the use of the digits 0–9, and of place value. His also made an important contribution to the spread of decimal numerals. He is considered “the most talented Western mathematician of the Middle Ages”.
#5 He INTRODUCED THE FIBONACCI SEQUENCE TO EUROPEAN MATHEMATICS
Fibonacci sequence is a series of numbers in which the next number is calculated by adding the previous two numbers. It goes like 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, and so on. Though the sequence had been described in Indian mathematics long ago, it was Leonardo Fibonacci who introduced the sequence to Western European mathematics. The sequence starts with F1 = 1 in Leonardo’s Liber Abaci but it can also be extended to 0 and negative integers like F0 = 0, F-1 = 1, F-2 = -1, F-3 = 2, F-4 = -3, F-5 = 5, and so on.

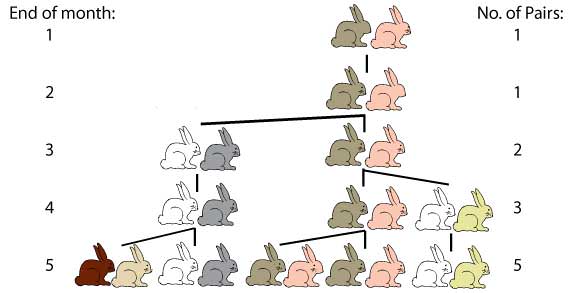
#6 FIBONACCI SEQUENCE WAS THE SOLUTION OF A RABBIT POPULATION PUZZLE IN LIBER ABACI
In Liber Abaci, Leonardo considers a hypothetical situation where there is a pair of rabbits put in the field. They mate at the end of one month and by the end of the second month the female produces another pair. The rabbits never die, mate exactly after a month and the females always produce a pair (one male, one female). The puzzle that Fibonacci posed was: how many pairs will there be in one year? If one calculates then one will find that the number of pairs at the end of nth month would be Fn or the nth Fibonacci number. Thus the number of rabbit pairs after 12 months would be F12 or 144.
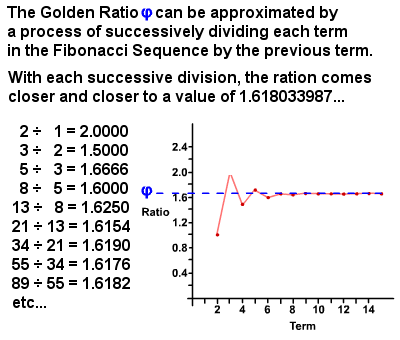
#7 FIBONACCI SEQUENCE IS RELATED TO THE GOLDEN RATIO
Two quantities are said to be in golden ratio if (a+b)/a = a/b where a>b>0. Its value is (1 + root 5)/2 or 1.6180339887… Golden ratio can be found in patterns in nature like the spiral arrangement of leaves which is why it is also called divine proportion. The proportion is also said to be aesthetically pleasing due to which several artists and architects, including Salvador Dali and Le Corbusier, have proportioned their work close to the golden ratio. The Fibonacci sequence and the golden ratio are intimately interconnected. The ratio of consecutive Fibonacci numbers converges and approaches the golden ratio and the closed-form expression for the Fibonacci sequence involves the golden ratio.
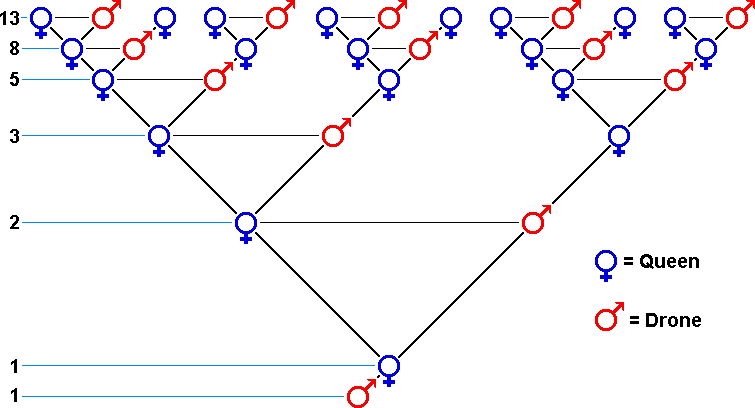
#8 FIBONACCI SEQUENCE IS FOUND IN THE ANCESTRY OF A DRONE BEE
Drones are male honey bees which are the product of an unfertilized egg. Since a drone has only one parent (only a mother and no father), it has an interesting genealogical tree. Generation 1 has 1 member (the male). One generation back there is also 1 member (the mother). Two generations back there are 2 members (the mother and father of the mother). It is found that the members in each generation going back is 1, 1, 2, 3, 5, 8, 13, 21…, they follow the Fibonacci sequence.
#9 FIBONACCI NUMBERS CAN BE FOUND IN SEVERAL BIOLOGICAL SETTINGS
Apart from drone bees, Fibonacci sequence can be found in other places in nature like branching in trees, arrangement of leaves on a stem, the fruitlets of a pineapple, the flowering of artichoke, an uncurling fern and the arrangement of a pine cone. Also on many plants, the number of petals is a Fibonacci number. Many plants including buttercups have 5 petals; lilies and iris have 3 petals; some delphiniums have 8; corn marigolds have 13 petals; some asters have 21 whereas daisies can be found with 34, 55 or even 89 petals.

#10 IT IS USED TO SEARCH A SORTED ARRAY IN COMPUTER SCIENCE
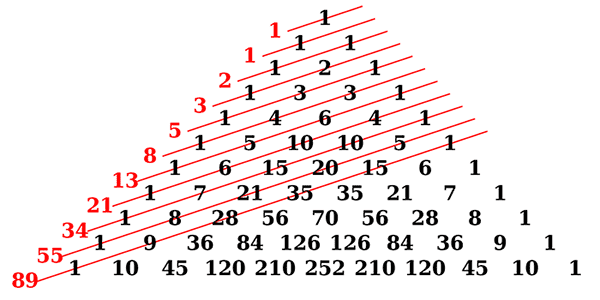
The Fibonacci numbers occur in the sums of “shallow” diagonals in Pascal’s triangle (see diagram below). Starting with 5, every second Fibonacci number is the length of the hypotenuse of a right triangle with integer sides. Fibonacci numbers are also an example of a complete sequence. This means that every positive integer can be written as a sum of Fibonacci numbers, where any one number is used once at most. Fibonacci sequence is used in computer science for several purposes like the Fibonacci search technique, which is a method of searching a sorted array with aid from the sequence.
FIBONACCI RETRACEMENT
Fibonacci retracement is a method of technical analysis which uses the Fibonacci sequence to determine at what point the price of a financial asset will stop and reverse in the opposite direction. Stock traders frequently take a cue from Fibonacci retracement to predict future share prices.


Love the information helped me out , thanks for taking the time on it.
Happy to help and you’re welcome